A Primer on Slowable Encoders
This article originally appeared on the NCC Group Cryptography Services blog.
There is a specific type of cryptographic transformation that arises in storage-oriented blockchains. The transformation is a “slowable” 1-1 mapping which does not involve any secrets and is tradeoff-resistant in the following sense: it should not be possible to partially compute the function, store some intermediate state significantly smaller than the function output, and then resume and finish the computation for anything less than the overall computation runtime cost.
In general, storage-oriented blockchains attempt to decentralize the traditionally centralized cloud data storage solutions. This is done by creating incentives for miners to store data and release it back to users for a fee. The underlying blockchain’s consensus algorithm requires miners to demonstrate they possess unique replicas of the data. Processing the data with a slowable encoding function throttles the miners’ ability to manipulate the consensus by reusing data served from a central data store, or reusing data they store multiple times (in order to increase their chances of winning the consensus).
In this blog post, we chat about the storage blockchain context and what motivates the need for such functions. We’ll detail on why some basic constructions based on CBC encryption mode previously discussed in [1] do not work. The fact that these constructions do not work can be seen as a doorway for research on how to build working and optimal ones - some of the papers that do that job are linked to by the end of this blog post. Therefore, this blog post can be seen as an introductory read for problems papers such as [1-5] are trying to solve.
Why encode before storing?
As mentioned, in decentralized storage blockchains, end-users can attempt to store data for a fee and miners are incentivized to store it for sufficiently long periods of time. Ideally, data should be stored in several replicas, to avoid data loss. The network should self-heal in the sense that, if the number of replicas for a particular piece of data becomes low, incentives exist for re-replicating the lost data pieces. All in all, miners are incentivized to store as many portions/chunks of the (ever-increasing) data blob as they can. The primary resource miners are competing with is storage space. The more chunks miners can store, the more likely is they will be able to win the upcoming block mining competition.
Some challenges in this context are:
- There needs to be a way of guaranteeing that storage providers are storing unique data replicas. A centralized storage solution may offer a data storage as a service and deliver it to miners for a fee, contrary to the intent of having as many data replicas as possible.
- Miners may be incentivized to store low-entropy (eg. all-zero) chunks as opposed to storing chunks with high entropy. Low-entropy chunks are advantageous, as they can be compressed efficiently, taking up minimal storage. When it’s time to use data chunks to participate in consensus, such chunks can be decompressed and sent to the network. This creates an incentive for storing dummy compressible data on the network which is contrary to the original intent- and that is to have a system which stores meaningful data.
Properties slowable encoders should satisfy
To deal with the problems above, storage-oriented blockchains came up with the following idea: miners do not compete with the exact chunk data, rather, they compete with encoded data, bound to unique identifiers and identities. Consider encoding data before storing it with a 1-1 function that produces random-looking (uncompressible) output, such that it satisfies the following properties:
- Slowable, ie. purposefully hard to compute (not parallelizable, memory hard, ASIC-resistant etc.)
- Tradeoff-resistant: any significant fraction of the function’s computation time should not be tradable for a fraction of the function’s (intermediate) state.
- Optionally, the data encoding may be slow in the forward direction and fast in the backward direction.
The first requirement prevents miners from encoding on the fly; for example, it should not be possible for a miner to download the data from a different provider in plaintext, quickly process it with the function and use it to participate in consensus. Alternatively, the centralized data provider may serve an already processed piece of data, however, that wouldn’t work as the identity of the miner is baked in the transformation. Finally, using a slow enough function should prevent storing data in a compressed format and processing it through the function when participating to the consensus.
For this work, it is also necessary for the function to be tradeoff-resistant in the following sense. It should not be possible to partially compute the function, store some intermediate state significantly smaller than the function output and then be able to resume the computation and finish it for a cost significantly lower than overall computation cost; otherwise, miners would be able to trade storage space for computation cost, which is essentially unwanted in this context. Finally, depending on the underlying protocol, the third property can help ease the computation workload on the parties that verify that providers actually do store the data.
Below are some primitives that do not satisfy such a tradeoff-resistance property:
- Use a stream cipher where the key initialization phase is computationally demanding and then derive as much keystream as required. The keystream is then XOR-ed with the data. If the inner state of the stream cipher is smaller in size than the desired keystream, a miner can compute the key initialization, store the cipher’s inner state and compute the keystream on the fly.
- The following (non-injective) computation:
H(D|1) | H(D|2) | H(D|3) | .. | H(D|n), whereDis data andHis a slowable hash function. Suppose the miner computes and stores a subset ofH(seed|i)blobs, achieving lower storage cost. The miner then computes the remainingHoutputs on the fly. - Use CBC-mode with a fixed publicly known key for each block and a slowable encryption primitive. A portion of the output can be saved and used to derive the remaining blocks.
Building slowable encoders
The following constructions mentioned in [1] build a data encoding function with an arbitrary input size from a smaller block encoder with fixed-size input \(E\). Both constructions are insecure, but iterating on them can result in secure ones. It should be mentioned that while the building block is a block cipher, there are no secrets in this context and all the “keys” are public values.
Consider a simple “layered CBC mode”. It depends on a constant, (publically known) key \(K\) and constant \(IV\) bound to the miner’s identity and context (unimportant for this discussion). If the data that’s being encoded is broken into blocks and the block sequence denoted with \(d_{0..N-1}\), we have:
\[c_0\ldots c_{N-1} = CBCEnc(IV, d_0\ldots d_{N-1})\] \[c_{(k+1)N}\ldots c_{(k+2)N-1} = CBCEnc(IV, c_{kN}\ldots c_{(k+1)N-1}), 0\leq k\leq l-1\]Considering each block to be a node in a graph, for 2-layer 8-block layered CBC mode, we have the following block dependency structure:
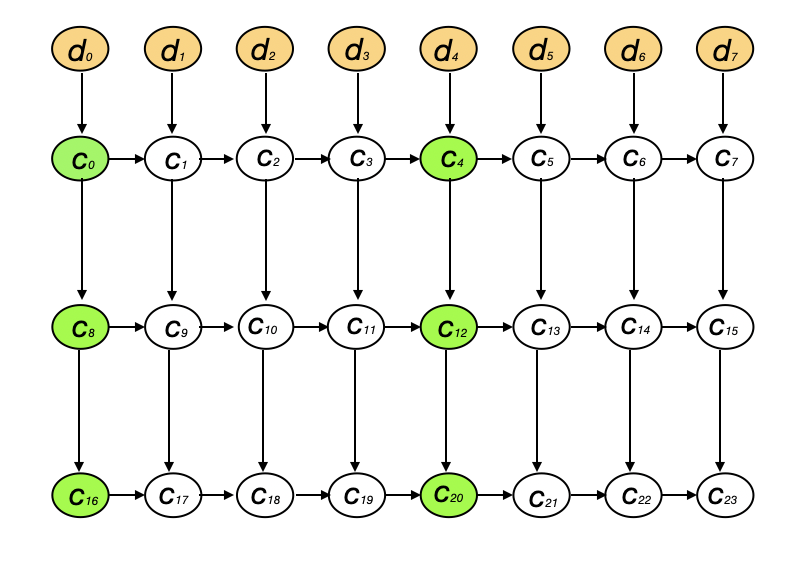
An honest storage provider is expected to store the bottom 8 blocks \(c_{16},\ldots c_{23}\). An adversary may instead store blocks \(c_4\), \(c_{12}\) and \(c_{20}\) and optionally store some of the \(c_0\), \(c_8\), \(c_{16}\) blocks (these blocks can be derived independently on the fly). The time to derive unknown blocks from the bottom should not be significantly smaller than recomputing all of the graph nodes.
Consider the cost of deriving for example block \(c_{23}\). First, observe that the derivation of that block can be localized inside the right-hand rectangle on the picture which starts from \(c_{4}\), \(c_{12}\) and \(c_{20}\). This already goes against the original intent, as the blocks from the left-hand rectangle do not need to be computed. Observe also that it is possible to derive blocks from that rectangle in parallel: first compute \({c_5}\) using one CPU, then compute \(c_{13}\) and \(c_6\) using two CPUs in parallel, finally compute \(c_{21}\), \(c_{14}\) and \(c_7\) in parallel using 3 CPUs and so on. Such parallelization is also an unwanted property, as it reduces the time needed to encode on the fly.
As such, there is too much regularity in the layered CBC mode construction. Let us try to remove some of it by adding a block permutation in between the layers. Denote the permutation on \(\{0,\ldots N-1\}\) with \(\pi\) and add it between layers:
\[c_{0..N-1} = CBCEnc(IV, d_{0..N-1})\] \[c_{(k+1)N}\ldots c_{(k+2)N-1} = CBCEnc(IV, c_{\pi(kN)}\ldots c_{\pi((k+1)N-1)}), 0\leq k\leq l-1\]This is similar to a block-cipher cipher construction where the base function \(E\) plays a role of an S-Box. Consider a 2-layer 8-block instance of this shuffled CBC mode with permutation \(\pi\) specified by the arrows on the picture:
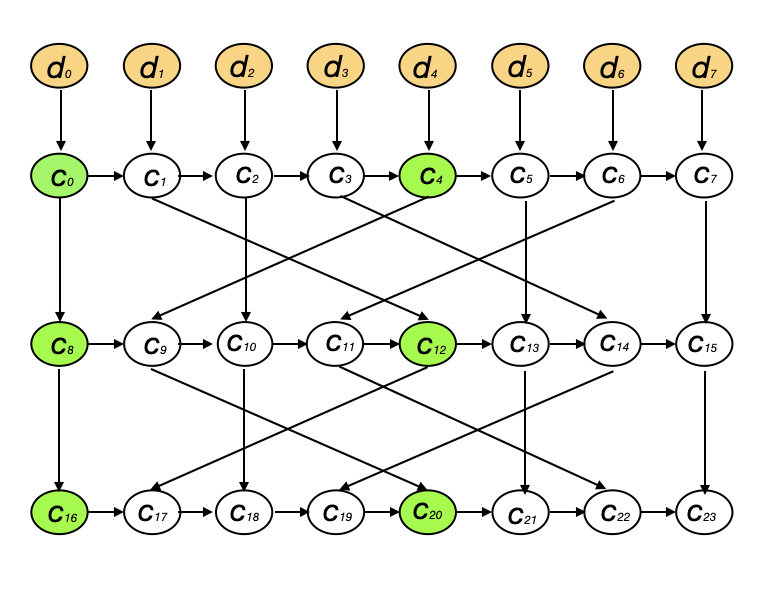
Suppose again an adversary stores the blocks colored in green. Consider how long it takes to compute \(c_{23}\), assuming a 2-CPU parallel computer. The computation of \(c_{23}\) now cannot be localized inside the right-hand rectangle and it depends on all blocks at all layers and re-deriving it appears harder. It is, however, still possible to parallelize the computation. Using the knowledge of \(c_0\) and \(c_4\), compute \(c_0,\ldots c_3\) and \(c_4,\ldots c_7\) in parallel, using 2 CPUs. Once the computation of \(c_0,\ldots c_7\) is complete, it is possible to do the same thing on the next level. Again, a lower than intended computation time is achieved.
The previously described issues may be remediated by adding more edges to the graph. Given specific function requirements (stemming from the upper layer, ie. the blockchain protocol), questions around constructing satisfactory graphs is a topic of a number of papers; for a sample, see [1-5]. In short, the desired final graph is constructed as an overlay of simpler graphs, including expander and depth-robust graphs. Below is a picture taken from [5], representing an example of a “stacked” Depth Robust Graph (DRG).
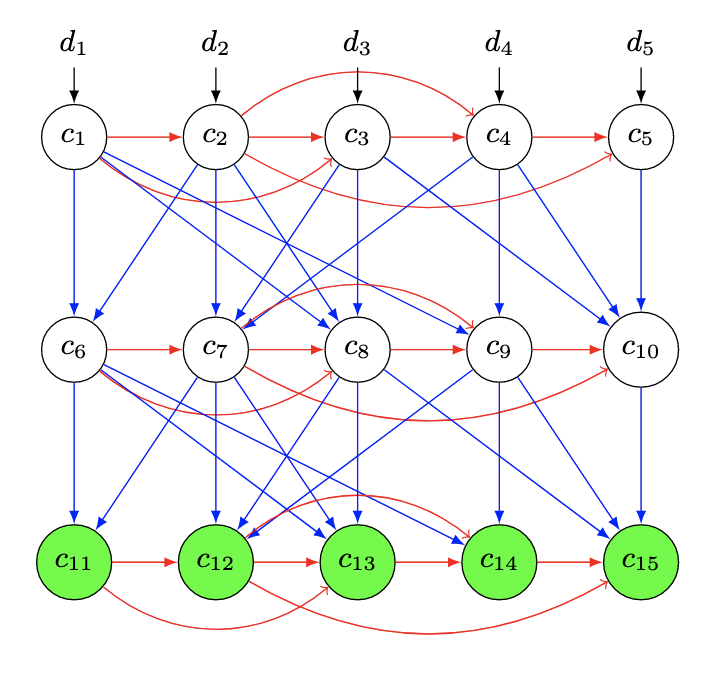
Due to the newly added edges, such constructions are expected to not suffer from issues similar to the ones previously described. When it comes to the data encoding function, it may be advantageous to use an encoding that’s slow in one direction, but fast in the other (decoding) direction. That way, validating the encoded blocks can be inexpensive for verifiers. Such functions include Sloth [5], a construction in the Verifiable Delay Function paper [6]; see also early proposals in the blockchain context [7]. Finally, it would be interesting to research how would randomly generated edges of same average length perform here, as opposed to a deterministic graph construction.
[1]: Scaling Proof-of-Replication for Filecoin Mining, Ben Fisch, Joseph Bonneau, Nicola Greco, and Juan Benet https://web.stanford.edu/~bfisch/porep_short.pdf
[2]: Proofs of Space, Stefan Dziembowski, Sebastian Faust, Vladimir Kolmogorov, Krzysztof Pietrzak, CRYPTO 2015 https://eprint.iacr.org/2013/796.pdf
[3]: Proof of space from stacked expanders, Ling Ren and Srinivas Devadas. TCC 2016 https://eprint.iacr.org/2016/333.pdf
[4]: Depth-Robust Graphs and Their Cumulative Memory Complexity, Joël Alwen, Jeremiah Blocki, and Krzysztof Pietrzak, EUROCRYPT 2017, https://eprint.iacr.org/2016/875.pdf
[5]: Tight Proofs of Space and Replication, Ben Fisch, EUROCRYPT 2017, https://eprint.iacr.org/2018/702
[5]: A random zoo: sloth, unicorn, and trx, Arjen K. Lenstra, Benjamin Wesolowski, International Journal of Applied Cryptography https://eprint.iacr.org/2015/366.pdf
[6]: Verifiable Delay Functions, Dan Boneh, Joseph Bonneau, Benedikt Bünz, and Ben Fisch, CRYPTO 2018 https://eprint.iacr.org/2018/601.pdf
[7]: Proof of unique blockchain storage, Sergio Demian Lerner, Blog post from 2014, https://bitslog.com/2014/11/03/proof-of-local-blockchain-storage/